使用单变量求解工具进行逆向敏感分析,首先需要建立正确的数学模型,这个数学模型通常与正向敏感分析时所使用的模型相同。
假设有一个简化的投资案例,”初始投资10万元,年收益率为10%,投资周期为15年,要求测算到期的资金总额及相关的收益情况。根据各个计算元素之间的关系建立表格,如图所示。
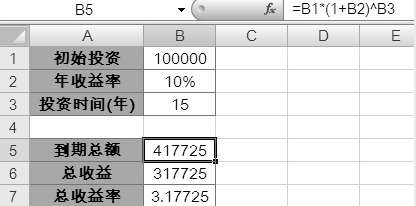
图中所有已知的初始条件分别位于B1:B3单元格区域中,而B5:B7单元格内是根据目前所提供的条件计算出的结果,其中B5单元格的公式为”=B1*(1+B2)^B3″。此公式是一个简单的复利计算公式,年收益按年累加得到最终的到期总金额。如果使用财务函数,也可以使用下面的公式:
B5=FV(B2,B3,,-B1)
B6单元格内的公式为:
B6=B5-B1
求得扣除投资本金以外的净利润。
B7单元格内的公式为:
B7=B6/B1
求得总的投资收益率。
建立完成这样的数学模型之后,对于正向预测分析的应用来说,只要在 B1:B3 单元格区域中更改参数条件,即可求得相应条件下的投资总收益情况。
假设用户现在需要了解,要在 15 年内将”总收益率”提升到 400%,至少需要保证每年多少的”年收益率”才能达到这个目标?这样的问题就是一个典型的逆向敏感分析需求,通过结果来求取条件。对于这样的分析需求,并不需要编写新的公式或创建新的数学模型,之前所建立的数学模型完全适用于使用单变量求解工具的逆向分析工程,方法如下。
选中 B7元格,在【数据】选项卡中依次单击【假设分析】→【单变量求解】命令,打开【单变量求解】对话框,如图所示。
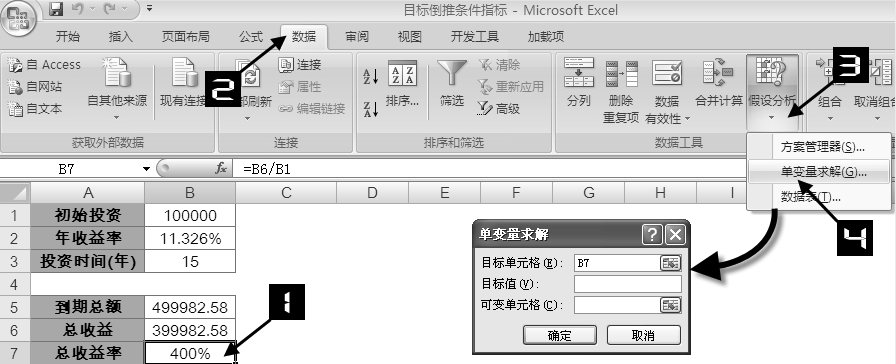
在【目标单元格】文本框中保持需要输入计算模型结果存放的单元格位置B7不变。
在【目标值】文本框中需要输入模型计算结果的具体取值。本例中的目标为”总收益率”达到 400%,因此在此处需要输入”400%”。
在【可变单元格】文本框中需要输入条件变量的单元格位置,即所要求取的条件因素所在位置。本例中需要求取”年收益率”,因此可在此处输入”B2″。用户也可以先将光标定位到文本框中,然后在工作表中选取 B2单元格,单元格地址会自动出现在文本框中。完成以上操作后的【单变量求解】对话框如图所示。
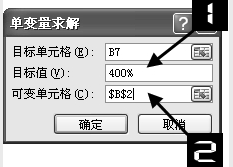
单击【确定】按钮,Excel立即开始运算过程,并在找到第一个解后中断运算过程,显示【单变量求解状态】对话框,如图所示。
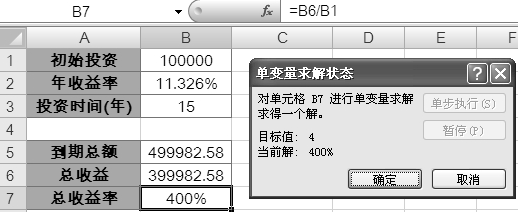
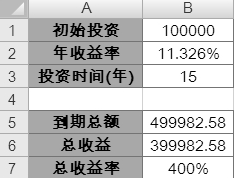
【单变量求解状态】对话框中显示当前单变量求解工具已经找到了一个满足条件的解,使得目标单元格达到目标值。其中”目标值” 指的是所设定的结果目标取值,而”当前解”则指当前Excel通过迭代计算所得到的目标单元格的结果,即 B7 单元格中的结果。在【单变量求解状态】对话框显示找到结果的同时,工作表中的条件单元格B2以及结果单元格区域B5:B7中也会同时显示当前取值下的结果。此时的”年收益率”显示11.326%,即表示在满足每年年收益率在11.326%以上的情况下,可以在15年后达到400%的”总收益率”目标。
单击【单变量求解状态】对话框中的【确定】按钮可以保留当前的单元格取值,如图所示。单击【取消】按钮或关闭此对话框则可恢复到运用单变量工具进行计算的工作表状态。
此技巧的介绍表明,要进行逆向敏感分析并不需要用户具备逆向思维和分析的能力(通常逆向思维比正向更困难),而只需通过预先建立的正向分析模型,借助Excel的单变量求解工具即可完成复杂的求解过程。

 iOS
iOS Android
Android Windows
Windows macOS
macOS